How does Pratt parsing works

While reading the book Building an interpreter in go from the great Thorsten Ball, one concept that blocked me for a while was the one about Pratt parsing and how it works. This article is meant to help people that are in the same situation I was in.

For this explaination, we are going to look at only parsing additions and multiplications with integers to understand the core of the algorithm. Once you understand these expressions, the rest is pretty self explainatory.

The initial parts

The first thing we are going to need for this algorithm is a table of precedence. Just like in regular mathematics, some operations need to be evaluated before other (PEMDAS).

The precendence table will look something like this

const PRECEDENCE = {
  LOWEST: 1,
  EQUALS: 2, // EQUALS
  LESSGREATER: 3, // > or <
  SUM: 4, // +
  PRODUCT: 5, // *
  PREFIX: 6, // -X or !X
  CALL: 7, // myFunction(X)
  INDEX: 8, // array indexes;
}

Next up, we are going to need a map of operators and their parsing function, for our simple example all we are going to need is this

// this is a pseudo code like implementation
registerPrefixFn(type: TokenType, fn: PrefixParseFn) {
  this.prefixParseFn.set(type, fn);
}

registerInfixFn(type: TokenType, fn: InfixParseFns) {
  this.infixParseFn.set(type, fn);
}

this.registerPrefixFn(TOKENS.INT, this.parseIntegerExpression);

this.registerInfixFn(TOKENS.PLUS, this.parseInfixExpression);
this.registerInfixFn(TOKENS.ASTERISK, this.parseInfixExpression);

Infix and prefix expression

Pratt parsing works by creating a tree like structure of node so that it can be evaluated easily. The lower in the tree a node is, the earlier it gets evaluated. Each node has an expression which is either an infix or prefix expression.

Prefix expressions, are for expression that need to be evaluated together, they only have a single arm which includes the value as well as the expression ex.: !true or -3

Infix expressions on the other hand have an operator and two arms ex.: 5 + 2

The parsing functions

Here is how we parse an integer

  parseIntegerExpression() {
    return new IntegerLiteral(this.currToken, Number.parseInt(this.currToken.Literal, 10));
  }

And here’s the implementation for the parsing of infix expression

parseInfixExpression(leftExp: Expression) {
    const token = this.currToken;
    const precedence = this.currPrecedence();

    this.nextToken();
    const rightExp = this.parseExpression(precedence);

    return new InfixExpression(token, leftExp, token.Literal, rightExp);
}

1. We save the current token
2. Get it’s precedence
3. Read the next token
4. Parse the right expression
5. return a new InfixExpression

The magic of the algorithm

This is were we get to the meat and potatoes of the algorithm, the parseExpression function is as followed

parseExpression(precedence: PRECEDENCES) {
    const prefix = this.prefixParseFn.get(this.currToken.Type);
    if (!prefix) {
      return;
    }

    let leftExp = prefix();


    while (this.peekPrecedence() > precedence
      && !this.peekTokenIs(TOKENS.SEMICOLON)) {
      const infix = this.infixParseFn.get(this.peekToken.Type);
      if (!infix) {
        console.log(`no infix for ${this.currToken.Literal}`);
        return leftExp;
      }

      this.nextToken();
      leftExp = infix(leftExp);
    }

    return leftExp;
  }

The algorithm can get messy if explained step by step like the other ones so I think it’s a better idea to explain the flow of thing rather than steps.

The idea is that we always start off parsing the left side of an expression, we then check if the precedence of the next token is higher than the one we received as argument and if that’s the case, we parse an infix function.

When we call the infix function, we pass the left expression as an argument which will then decide if the expression belongs in the first of second node. This is what some people describe as “biding power” or “stealing” when they talk about Pratt parsing.

For example, if we had 3 + 6 * 8. When we get to parsing 6, we have to know where it belong

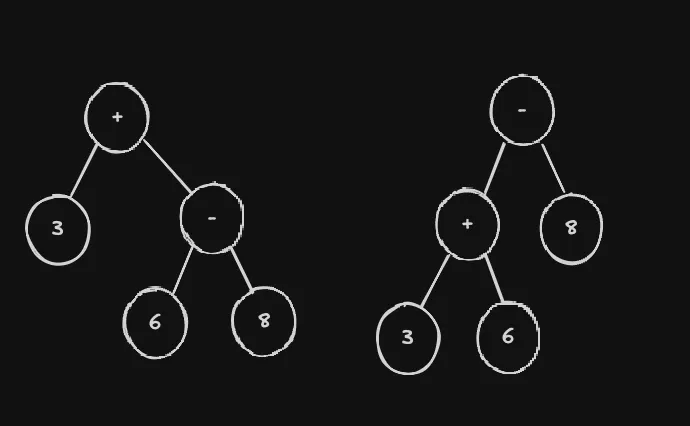
The answer is the first one, since the multiplication has higher binding power, it enter the while loop and doesn’t return immediatly so it “steals” it. If we had it the other way around, 8 * 6 + 3 in that case, once the 6 would get passed to next expression leftExp = infix(leftExp), we would never enter the while loop and immediatly return the value.

It might be a better to say, instead of stealing a value, we pass the value to the next expression and it either decides to return it or keep it. The idea is to make it clear that the function is parsed and then passed around and not “stolen”.

Once you understand that, the rest is pretty self explanatory since the only thing that changes is the parsing expression. Each parsing function calls the main parseExpression function with it’s own precedence level and we end up with a fully parsed tree of nodes.